Goldberg polyhedron

Zdroj: https://en.wikipedia.org/wiki/Goldberg_polyhedron

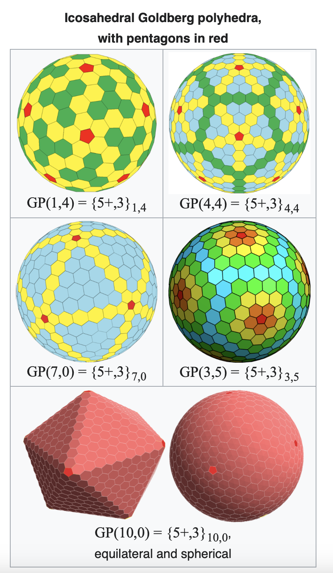
Ikosaedrický Goldbergův mnohostěn s červeně znázorněnými pětiúhelníky

GP(1,4) = {5+,3}1,4
GP(4,4) = {5+,3}4,4

GP(7,0) = {5+,3}7,0
GP(3,5) = {5+,3}3,5

GP(10,0) = {5+,3}10,0,
rovnostranný a kulový

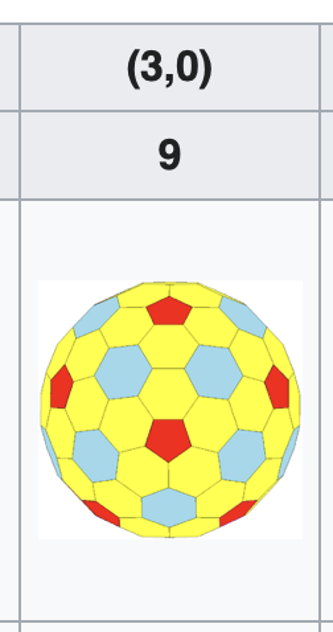
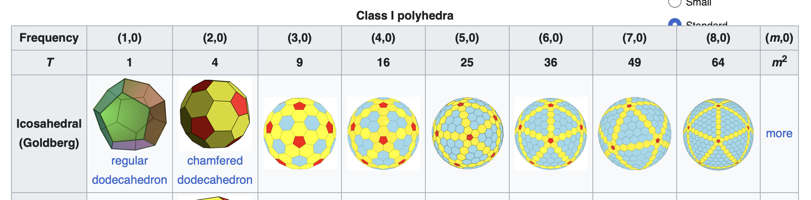
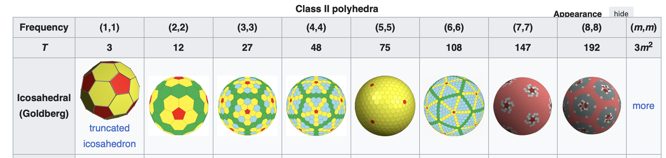
V matematice, a konkrétněji v polyedrické kombinatorice, je Goldbergův mnohostěn konvexní mnohostěn složený z šestiúhelníků a pětiúhelníků. Poprvé je popsal v roce 1937 Michael Goldberg (1902–1990). Jsou definovány třemi vlastnostmi: každá stěna je buď pětiúhelník, nebo šestiúhelník, v každém vrcholu se setkávají přesně tři stěny a mají rotační ikosaedrickou symetrii. Nemusí být nutně zrcadlově symetrické; např. GP(5,3) a GP(3,5) jsou enantiomorfy jeden druhého. Goldbergův mnohostěn je duální mnohostěn geodetického mnohostěnu.

Důsledkem Eulerova vzorce pro mnohostěn je, že Goldbergův mnohostěn má vždy přesně 12 pětiúhelníkových stěn. Dvacetistěnná symetrie zajišťuje, že pětiúhelníky jsou vždy pravidelné a že jich je vždy 12. Pokud vrcholy nejsou omezeny na kouli, lze mnohostěn sestrojit s rovinnými rovnostrannými (ale obecně ne rovnoúhlými) stěnami.

Mezi jednoduché příklady Goldbergových mnohostěnů patří dvanáctistěn a komolý dvacetistěn. Jiné formy lze popsat tahem šachového jezdce z jednoho pětiúhelníku do druhého: nejprve udělejte m kroků jedním směrem, poté se otočte o 60° doleva a udělejte n kroků. Takový mnohostěn se označuje GP(m,n). Dvanáctistěn je GP(1,0) a komolý dvacetistěn je GP(1,1).

Vychází tedy z Archimédovského tělesa komolého dvacetistěnu - https://cs.wikipedia.org/wiki/Archimédovské_těleso 

Ale proč to mám u Santiniho a jeho Zelené hory?

Protože pentagon s hexagonem propojíme z vnější strany pomocí triquetry, ale ve středu je propojíme pomocí Květu života!