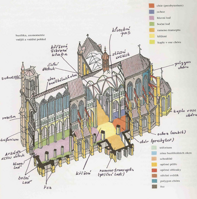
Základy posvátné geometrie
Jak to vypadá, když Indiana Jones potká Santiniho na vlakovém nádraží?
Exkluzivní obsah a nové články najdete na HeroHero (Tania, Alchymistka-Tania's Secret) .
Obsah zdarma je umístěný také na YouTube - Alchymistka - Tania's Secret
Facebooková stránka: Tania's Secret: Papoušek mezi světy
Tao říká:
"Tao rodí jedno,
jedno rodí dvě,
dvě rodí tři
a tři rodí všechny bytosti."
Povíme si to jako příběh, rozprávku, prostě legendu, mýtus, pohádku...
Pokud došlo k Velkému třesku (a ono zřejmě ano, i když nevíme jak), tak první, kdo byl zrozený, byl Jeden. Je to jako první den, první Bůh, první nádech...Prostě ten Jeden jediný prvorozený...
Mohl to být egyptský bůh Ra? Můžeme mu tak říkat. Bůh Slunce Ra... Každá mythologie na Zemi mu říká jinak, u každé se příběh může i jinak odvíjet..., ale máme to i ve Fibonacciho spirále, na začátku (hned za nulou, nulovým bodem, bodem nestvořené a bodem neexistence) máme číslo 1.

Egypstký bůh Ra (wikipedie)

Tao rodí jedno
1
Máme tedy myšlenku pro vznik prvního kruhu, ze kterého bude následovat postupným přidáním dalších kruhů celý Květ života, coby grafické vyjádření Základního vzorce tohoto stvořeného světa, ve kterém žijeme.
První kruh, první krok, první nádech, první Bůh, první Stvořitel. Kruh může být také vyjádřený písmenem Pí, jehož hodnota je zhruba 3,14.
Jedno rodí dvě
2
Dvě Pí (2 x 3,14), alias písmeno Tau, vytvoří bránu.
Brána je vesica piscis alias mandorla, alias božský průzor alias nebeská brána...
První dvě kružnice, první dva kruhy z budoucího Květu života.
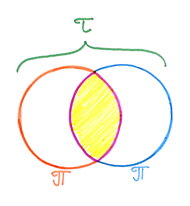
Dvě rodí tři
3
Triquetra (i trikvetra), je latinský výraz pro "tři rohy", ve skutečnosti to znamená rovnostranný trojúhelník.
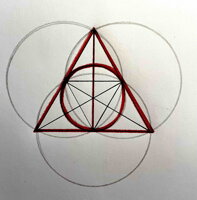
Triquetra je ta silně černě vyznačená a získáme jí ze tří kružnic/kruhů.
Na barevném obrázku jsou vyznačeny rovnostranné trojúhelníky.
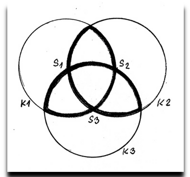
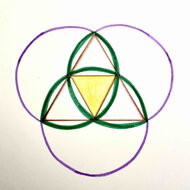
Keltské uzly triquetra (wikipedie).
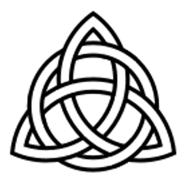
Rovnostranný trojúhelník - tečny, kružnice opsaná a vepsaná - obrázek vlevo.
Relikvie smrti z filmů o Harrym Potterovi - obrázek vpravo.
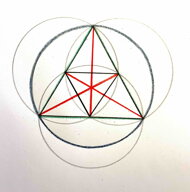
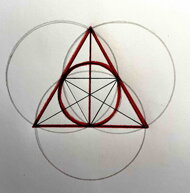
Tři rodí všechny bytosti
Tři je ona triquetra.
4 - čtverec
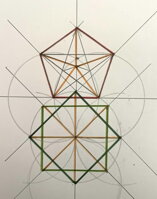
Pomocí triquetry narýsujeme čtverec (červeně vyznačený, triequetra je modrá).
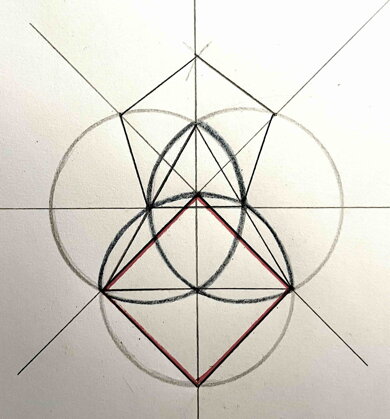
5 - pětiúhelník, pentagram, pentagon
Pomocí triquetry narýsujeme pentagon a pentagram.
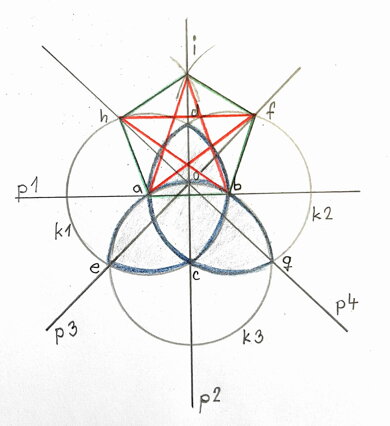
Pomocí triquetry narýsujeme i hexagon a hexagram.
6 - šestiúhelník, hexagram, hexagon
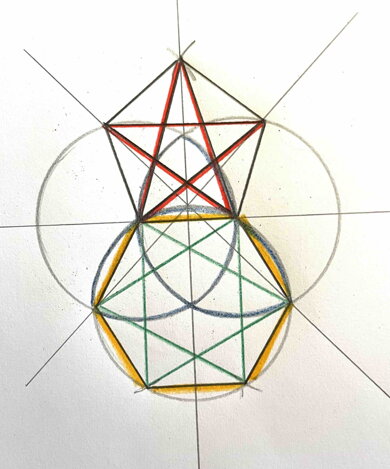
Záhady a Teslových 3-6-9
Už jsme si ukázali, jak můžeme pomocí vesici piscis a triquetry narýsovat jak čtverec a hexagram, ale i pentagram.
Co bychom si měli připomenout a uvědomit.
Číslo 9
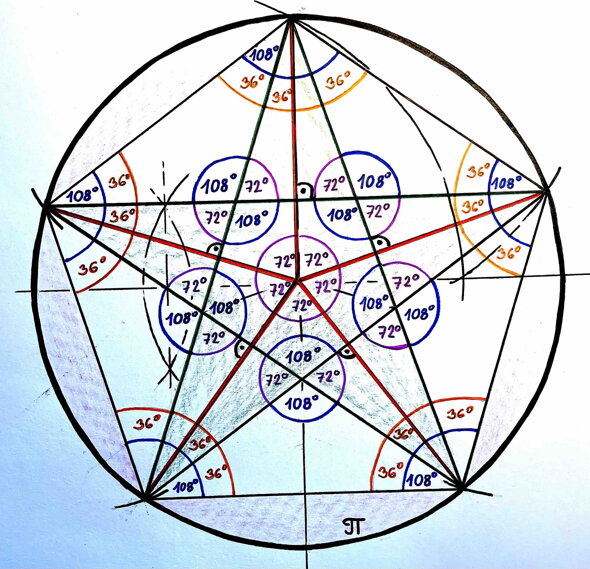
Úhly v pentagramu, když je všechny sečtete, získáte číslo 9.
Pentagram vzniknul z triquetry.
Triquetra je číslo 3.
Z triquetry můžete narýsovat čtverec.
Úhly ve čtverci mají hodnotu 90°. Když tuto hodnotu sečtete, získáte číslo 9.
Rovnoramenné trojúhelníky narýsované pomocí triquetry, které se nacházejí ve čtverci, který jsme pomocí triquetry narýsovali (a oněch trojúhelníků) mají velikost úhlu u základny 45° a u vrcholu velikost úhlu 90°. Když sečtete 45° dostanete číslo 9.
Z triquetry můžete narýsovat hexagram (dva trojúhelníky v sobě) a hexagon.
Hexagram je tvořený dvěma protilehlými rovnostrannými trojúhelníky, jejichž vnitřní úhly mají vždy hodnotu 60°. Po součtu tedy získáte hodnotu 6.
To znamená, že zde máme jeden ze způsobů vyjádření Teslových čísel 3-6-9.
Triquetra = 3
Hexagram ze dvou rovnostranných trojúhelníků triquetry (3) je spojen s číslem 6.
Pentagram a pentagon obsahuje všechny úhly o součtové hodnotě velikosti 9.
Triquetra - hexagram - pentagram = 3 - 6 - 9